Sólo para Socios:
Boris Ryabko y Zhanna Reznikova
Enviado y traducido por el socio José María Gómez Durán: Agradezco
a
“Using Shannon Entropy and Kolmogorov Complexity to study the communicative system and cognitive capacities in ants”. Los trabajos de Z. Reznikova no sólo han abierto un campo nuevo en el estudio del lenguaje y las capacidades cognitivas de las hormigas; constituyen, de hecho, un inédito enfoque metodológico para la investigación del comportamiento inteligente. Fruto de estos trabajos y de esta nueva perspectiva es su reciente libro "Animal
Intelligence: From Individual to Social Cognition" (Cambridge University
Press, 2007).
B. Ryabko es Jefe del Departamento de Matemática y Cibernética Aplicada de
Z. Reznikova es Jefa del Departamento de Psicología Comparada de
Introducción
Los sistemas de comunicación de los animales, así como sus capacidades cognitivas, han sido tema de investigación de especial interés para biólogos, psicólogos, lingüistas y muchos otros, incluyendo los investigadores del campo de la robótica. Durante las últimas tres décadas se han desarrollado novedosas aproximaciones experimentales, como las basadas en el diálogo directo con animales adiestrados en lenguajes artificiales intermediarios [1-4]. Se ha podido demostrar que los primates no sólo son capaces de tomar decisiones, de realizar operaciones de generalización y extrapolación, sino también de usar reglas gramaticales muy sencillas y símbolos visuales tales como lexigramas, letras y números [5-6]. El conteo y las capacidades relacionados con los números se ha demostrado en el loro gris [7]. Se ha creído durante mucho tiempo que la actividad cognitiva sólo es posible en los vertebrados; sin embargo, los experimentos de Mazokhin-Porshnyakov [8, 9] han demostrado que las abejas y las avispas sociales son capaces de abstracción, extrapolación y resolución de tareas bastante complicadas.
La cuestión de la existencia de un lenguaje natural desarrollado en algunas especies de animales sociales, continua poco clara. El más complejo de los lenguajes naturales animales conocidos es la danza simbólica de la abeja melífera, basado en un sistema de localización a distancia. Esta intrincada forma de comunicación fue descubierta por K. von Frisch [10], y desde entonces ha sido estudiada intensamente empleando diferentes métodos [11, 12].
La actividad señalizadora en las hormigas ha atraído también la atención de muchos investigadores. Se sabe que las hormigas son capaces de utilizar una gran variedad de formas de comunicación para reclutar hacia una fuente de alimento [13]. Durante mucho tiempo no ha quedado claro si tenían un sistema de localización a distancia. En este sentido, el denominado “código” táctil (o antenal) ha sido discutido extensamente. Una hipótesis relativa a la existencia de tal sistema de transmisión de información en las hormigas fue propuesto por E. Wasmann en fecha tan temprana como 1899 [14]. Sin embargo, los numerosos intentos de descifrar el “lenguaje” de las hormigas no ha dado los resultados esperados [15, 16]. La capacidad de las hormigas para resolver problemas lógicos y para transmitir información compleja por medio de un sistema de localización a distancia, ha sido demostrada por Reznikova [17-19]. Pero nada se sabía sobre las aptitudes de lenguaje involucradas.
Las principales dificultades en el análisis del lenguaje animal son las metodológicas. Muchos estudiosos han intentado descodificar el lenguaje animal buscando “letras” y “palabras”, y compilando “diccionarios”. Con una aproximación de este tipo no suele quedar claro qué sonidos y gestos tienen relación con el lenguaje y cuáles no, existiendo al mismo tiempo algunos problemas técnicos vinculados a la gran movilidad de los animales y, frecuentemente, a la dificultad para registrar los signos. El hecho de que los científicos sólo hayan conseguido compilar diccionarios de la abeja de la miel indica, no que otros animales carezcan de lenguaje, sino que faltan los métodos adecuados.
A finales de la década de 1940 C. Shannon desarrolló la base de la Teoría de la Información [20]. El papel fundamental de esta teoría fue apreciado inmediatamente, no sólo en el desarrollo de la tecnología de transmisión de información, sino también en el estudio de los sistemas naturales de comunicación. Es lógico emplear la teoría de la información en la investigación de los sistemas de comunicación porque esta teoría expone principios generales y métodos para desarrollar sistemas de comunicación efectivos y fiables. En particular, en la década de 1950 y 1960 se estimaron las entropías (grado de incertidumbre y diversidad) de la mayoría de los lenguajes europeos. Más tarde, las ideas de la teoría de la información entraron en el campo de la fisiología. Por ejemplo, el tiempo de reacción humano bajo condiciones experimentales resulto ser proporcional a la incertidumbre presente en el experimento [21]. Sorprendentemente, la aplicaciones de la teoría de la información sólo se han incorporado a unos pocos estudios. Así, la teoría de la información fue empleada en la estimación de los parámetros cuantitativos de la capacidad de la abeja de la miel para memorizar la localización de una fuente de alimento [22].
Describimos aquí una aproximación muy diferente para el estudio de la comunicación y cognición animal basada en las ideas de la entropía de Shannon y la complejidad de Kolmogorov. Esta aproximación ha permitido ya demostrar la existencia de una inteligencia y lenguaje desarrollados en algunas especies de hormigas altamente sociales. Los principales resultados han sido publicados en revistas de biología [23-25] y anunciadas y discutidas en congresos internacionales [26-29].
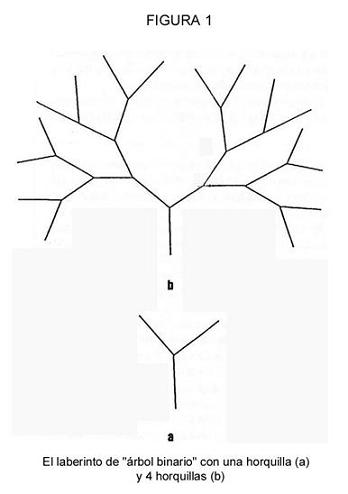
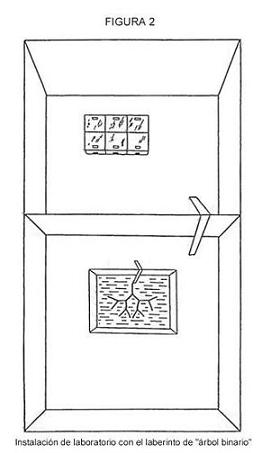
El elemento principal de esta aproximación es que nuestros experimentos generan una situación en la que las hormigas tienen que transmitir una información, cuantitativamente conocida por el experimentador, para conseguir alimento. Esta información tiene que ver con la secuencia de giros a realizar en dirección a un bebedero con sirope. Utilizamos una nueva instalación de laboratorio denominada “árbol binario”, donde cada “hoja” del árbol termina en un bebedero vacío, con la excepción de uno lleno con sirope. El diseño más sencillo era el árbol con dos hojas y dos bebederos, estando el sirope sólo en uno de ellos [Figura 1(a)]. En esta situación, una hormiga exploradora transmitiría un bit de información a las forrajeadoras: ir hacia la derecha o hacia la izquierda. En otros experimentos el número de horquillas en una rama se incrementaba hasta seis [La Figura 1(b) muestra una instalación con cuatro horquillas]. Por tanto, el número de bits necesarios para elegir el camino correcto era igual al número de horquillas. La secuencia de giros fue escogida al azar lanzando una moneda. La instalación se hizo con tiras (de 50 mm) y bolas (de 10 mm) de plástico. Para evitar el acceso directo al alimento en línea recta, la instalación se colocó en un recipiente con agua (600 x 600 mm), Las hormigas alcanzaban en punto inicial del árbol caminando sobre un puente (Figura 2).
La utilización de las ideas de la entropía de Shannon permitía la existencia de un número potencialmente ilimitado de mensajes en el lenguaje de las hormigas, que había que demostrar. Igualmente, se hacía necesario estimar la tasa de transmisión de la información (aproximadamente 1 bit/minuto). También tuvimos éxito al estudiar algunas propiedades de la inteligencia de las hormigas, singularmente su capacidad para memorizar y usar regularidades sencillas comprimiendo la información disponible. Los últimos experimentos se basaron en las ideas de la complejidad de Kolmogorov. Creemos que los esquemas experimentales descritos pueden usarse para estudiar los sistemas de comunicación de otros animales.
Descripción de los experimentos
Los experimentos se realizaron desde 1982 en tres especies de hormigas, cada una de ellas con un alto grado de organización. Las hormigas estaban alojadas en el laboratorio dentro de una plataforma de 2 x 2 metros, en un nido transparente. Las colonias contenían entre 800 y 2000 individuos. Todas las hormigas experimentales fueron marcadas con señales de colores y alimentadas una vez cada tres días (únicamente en la instalación experimental).
En todas las series de experimentos con el laberinto de árbol binario, las hormigas fueron alimentadas durante 10-12 días en el modelo con una sola horquilla. En estos casos las forrajeadoras partían del nido como consecuencia de una excitación e imitación colectiva. El comportamiento de las hormigas cambiaba radicalmente si el bebedero con sirope estaba situado en una de las cuatro hojas del segundo giro del árbol binario, lo que hacía más complicada su tarea.
La colonia de laboratorio incluía “equipos” que consistían en una exploradora y entre 5 y 8 reclutadas: la exploradora sólo atraía a su equipo hacia el alimento. Los equipos se descubrieron en experimentos especiales preliminares. No todas las exploradoras conseguían memorizar el camino hacia el laberinto; además, el número de tales exploradoras disminuía con la complicación de la tarea: por ejemplo, en el caso de dos horquillas todas las exploradoras activas y sus grupos seguían trabajando, mientras que en el caso de seis horquillas sólo trabajaban una o dos. En total, se emplearon en nuestros experimentos más de 200 equipos de tres especies de hormigas.
Durante los experimentos colocamos exploradoras en el bebedero que contenía el alimento, y la exploradora volvía al nido por su cuenta. Algunas veces la exploradora contactaba con su equipo a la primera, y el grupo comenzaba a desplazarse hacia la instalación. En este caso, después de que la exploradora contactara con las forrajeadoras, aislábamos a la exploradora para que las forrajeadoras tuvieran que buscar la comida por sí mismas. Pero más a menudo, después de que la exploradora llegara al nido, lo abandonaba y retornaba sola al bebedero. Algunas veces cometía errores, y sólo encontraba el bebedero con alimento después de visitar algunos vacíos. Entonces volvía al nido otra vez, contactaba con el equipo y, o se quedaba con el equipo, o lo abandonaba. En el primer caso se aislaba a la exploradora, mientras en el segundo caso realizábamos el experimento repetidamente. Algunas veces la exploradora tenía que hacer hasta cuatro viajes antes de poder movilizar a las forrajeadoras. En todos los casos de movilización medíamos la duración (en segundos) del contacto entre la exploradora y las forrajeadoras en el nido. Considerábamos que se iniciaba el contacto cuando la exploradora tocaba a la primera hormiga forrajeadora, tomando como final del contacto el momento en que el nido era abandonado por las dos primeras forrajeadoras. A los contactos sucedían frecuentemente numerosos movimientos antenales. Las exploradoras contactaban con una a cuatro forrajeadoras de forma sucesiva, a veces con dos simultáneamente. Cuando la exploradora volvía repetidamente sola al bebedero, medíamos cada uno de sus contactos con las forrajeadoras. Sólo se tomaba en cuenta la duración del último contacto que precedía al abandono del nido por parte de las forrajeadoras. Por lo general, todos los contactos previos eran breves (de 1 a 5 seg.) y orientados al intercambio de alimento.
En cada serie de experimentos con el bebedero situado en la i-hoja del árbol binario, trabajaban sucesivamente todos los grupos de forrajeadoras activas aquel día (de uno a cinco). Durante el ensayo, retirábamos el puente que conducía al área de trabajo de la instalación, con el objeto de evitar que acudieran allí miembros de otros equipos.
Los experimentos fueron ideados para eliminar cualquier posible ayuda que pudiera facilitar el hallazgo del alimento, exceptuando la proveniente de la localización a distancia, es decir, la información procedente del contacto con una hormiga exploradora. Durante el contacto en el nido entre una exploradora y las forrajeadoras, la instalación experimental era reemplazada por otra similar para evitar el uso de una pista olorosa. Para evitar tanto la pista como el olor del alimento, se llevaron a cabo una serie especial de experimentos. Mientras la exploradora estaba en el interior del nido, reemplazábamos el laberinto completo con uno nuevo con todos los bebederos vacíos. De esta forma, tras los contactos con la exploradora, las forrajeadoras visitaban bebederos vaciados a propósito. Tales experimentos los llamábamos “exámenes”. Las hormigas eran alimentadas durante los intervalos entre dichos exámenes, pero sin disponer de alimento en ningún examen en particular.
Entropía de Shannon y Transmisión de Información en las Hormigas
En nuestros experimentos los grupos de forrajeadoras, después de un contacto con la exploradora, encontraban el cebo sin equivocarse la mayoría de las veces. La Tabla 1 da los resultados de los exámenes, en los cuales las hormigas visitaban el laberinto tras haberse colocado allí los bebederos vacíos. Probaremos primero la existencia de transmisión de información en las hormigas. Comparamos la Hipótesis H0 (las forrajeadoras ocasionalmente encuentran un bebedero) con la Hipótesis H1 (encuentran la comida gracias a la información recibida). La probabilidad de encontrar al azar el camino correcto hacia el bebedero en el laberinto de tres horquillas es (1/2)3. La tabla 1 muestra que en tres casos (líneas 2, 3, 4) los grupos de forrajeadoras no encontraron el alimento; en cinco casos (líneas 8, 9, 10, 12, 19) de una a tres hormigas quedaron atrás del grupo, y en 12 casos todas las forrajeadoras alcanzaron correctamente las hojas donde sus exploradoras encontraron alimento. En estos experimentos una búsqueda acertada se consideraba un éxito, mientras que una búsqueda infructuosa, cuando el equipo erraba al llegar o llegaba en pequeño número, se consideraba un fracaso.
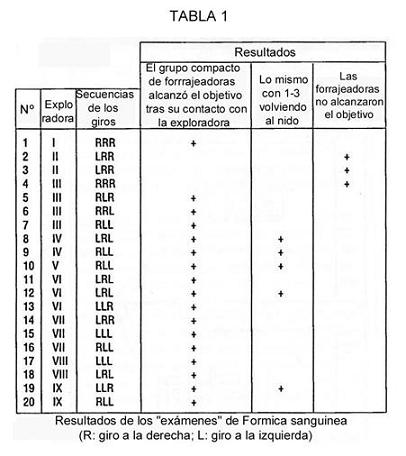
Así, tenemos los resultados de 20 test independientes de Bernouille, donde la probabilidad de éxito (P) en caso de cumplirse H0 es (1/2)3, frente a H1, donde P>1/8. Hubo 12 éxitos y 8 fracasos. Para verificar H0 frente a H1 utilizamos el criterio binomial (ver las tablas en [30]). En nuestro caso, H0 fue rechazada en favor de H1, P < 0.001. Por tanto, los datos obtenidos mostraron que las hormigas no habían utilizado olores de pistas o del alimento (nótese que habíamos sustituido el laberinto y que los bebederos estaban vacíos). Además, esta tabla muestra la capacidad de la exploradoras, durante un experimento, para transmitir información sobre rutas hacia el cebo totalmente diferentes (por ejemplo: líneas 9-10, 11-13, 14-16, etc.). De modo que las hormigas no pudieron hacer uso de experiencia previa.
Aparte del análisis estadístico del número de llegadas exitosas al objetivo por parte de un grupo, llevamos a cabo experimentos de control en los que las hormigas eran introducidas a propósito en el laberinto, sin contactos con una exploradora. Se les permitía buscar alimento durante 30 minutos. Si el laberinto tenía tres o más giros, normalmente fracasaban en su intento de encontrar el alimento durante ese periodo. Esas hormigas, al buscar el camino hacia su nido, a menudo volvían al puente y comenzaban a explorar de nuevo. Adviértase que en todos los experimentos se introducían exploradoras a propósito dentro el laberinto, dado que la inspección que hacían de las hojas para encontrar el alimento solía fracasar.
La cantidad de información (en bits), necesaria para escoger el camino correcto en el laberinto, es igual a i, el número de horquillas. Asumimos que la duración de los contactos entre las exploradoras y las forrajeadoras (t) era ai + b, donde i es el número de horquillas, a el coeficiente de proporcionalidad, igual a la tasa de transmisión de la información (en bits/minutos), y b era la constante introducida, ya que las hormigas pueden transmitir información no directamente relacionada con la tarea; por ejemplo, la señal sencilla “alimento”. Además, no queda descartado que una hormiga descubridora transmita, de alguna manera, la información sobre su ruta hacia el nido utilizando comunicación acústica o de algún otro tipo. Para nosotros es importante destacar que el camino desde el laberinto hasta el nido era aproximadamente el mismo en todos los experimentos; por tanto, el tiempo anterior al contacto antenal con las forrajeadoras en el nido, que la exploradora podría usar hipotéticamente para la transmisión de mensajes, era aproximadamente el mismo y no dependía del número de horquillas.
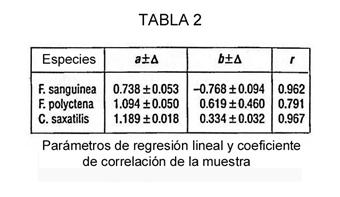
Con los datos obtenidos evaluamos los parámetros de regresión lineal y el coeficiente de correlación de la muestra (r) (Tabla 2). En todos los casos, la correlación entre la duración de los contactos y la cantidad de información (el número de horquillas i) resultó ser cercana a la linealidad, probablemente debido al alto valor del coeficiente de correlación de la muestra (Tabla 2). Todos los valores del coeficiente de correlación diferían significativamente de 0 para P = 0.01.
En tres especies de hormigas la tasa de información transmitida (a), derivada de la ecuación t = ai + b, es 0.738, 1.094 y 1.189 bits/minuto, respectivamente. No consideramos estos valores como constantes específicas; probablemente varían. Debe mencionarse que estos valores son, en casi un orden de magnitud, más bajos que los de la comunicación humana [21].
Consideremos ahora el número total de caminos diferentes posibles hacia el bebedero. En el árbol binario más sencillo, con una horquilla, hay dos hojas y, por tanto, dos caminos diferentes. En un árbol con dos horquillas hay 22 caminos; con tres horquillas, 23 caminos; y con seis horquillas, 26 caminos; así, el número total de caminos diferentes es igual a 2 + 22 +23 + …. + 26 = 126. Este es el número mínimo de mensajes que deben manejar las hormigas para resolver una tarea mediante el sistema de localización a distancia.
Complejidad de Kolmogorov e Inteligencia de las Hormigas
La capacidad para captar rápidamente las regularidades y usarlas en la codificación y “compresión” de la información, debería considerarse como una de las propiedades más importantes del lenguaje y de la inteligencia que comporta. Así, la longitud del texto sería proporcional a la complejidad de la información. Esta idea es un concepto básico de la complejidad de Kolmogorov. Este concepto se aplica a las palabras (o texto) formado por las letras del alfabeto; por ejemplo, de un alfabeto consistente en dos letras, L y R.
Dicho de manera informal, la complejidad de una palabra (y su incertidumbre) es igual a la longitud de su descripción más concisa, de acuerdo con Kolmogorov. Por ejemplo: la palabra “LLLLLLLL” puede representarse como “8L”, la palabra “LRLRLRLR” como “4LR”, mientras que la palabra “aleatoria” de menor longitud “LRRLRL” probablemente no puede expresarse de forma más concisa. Por tanto, la primera palabra es la más sencilla y con menor incertidumbre, la segunda es más compleja, y la tercera es la de mayor complejidad e incertidumbre. Intentamos analizar la cuestión de si las hormigas pueden emplear regularidades “textuales” sencillas para su compresión (aquí, “textual” significa la secuencia de giros en el laberinto).
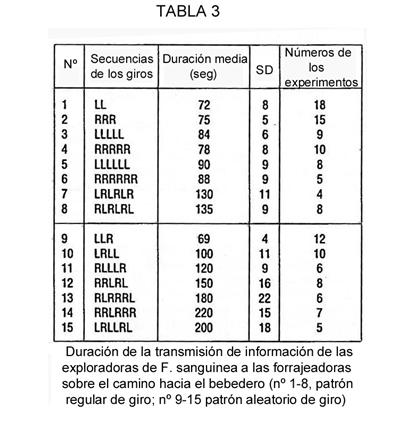
Como demostró Kolmogorov [31], no existe una medida cuantitativa, algorítmicamente evaluada, de la complejificación textual. Por ello, estrictamente hablando, sólo podemos verificar si las hormigas y los humanos tienen la misma noción acerca de los textos sencillos y complejos. En la serie especial de experimentos, se les presentó a las hormigas las siguientes secuencias de giros, reflejadas en la Tabla 3. Evidentemente, la mayoría de las personas percibe la secuencia de horquillas de la 5ª y 6ª líneas de la Tabla 3 como más sencillas que las de la 7ª y 8ª líneas, las cuales, a su vez, son más sencillas que las aleatorias de igual longitud (líneas 13-15). La cantidad de tiempo empleado en la transmisión de información entre las hormigas, en relación con la secuencia de horquillas, se incrementaba con la complicación de la tarea (líneas 5-8 y 13-15).
Esto pudo probarse estadísticamente. Comparamos la hipótesis principal H0 –el tiempo de transmisión de la información no depende de la complejidad del texto–, con la hipótesis H1 –dicho tiempo sí depende de la complejidad textual–. Este experimento consistió en siete series con secuencias de giros de igual longitud (Tabla 3: líneas 5-8 y 13-15). El número total de órdenes de secuencias de giro, de acuerdo con la duración de la transmisión, es 7!, de las cuales 2!2!3! concuerdan con H0. La probabilidad de obtener un orden de este tipo de acuerdo con H0 es muy pequeña: 2!2!3!/7! = 1/120. Así, concluimos que la hipótesis H1 se ha cumplido: mientras más sencillo es un texto, menos tiempo se emplea en la transmisión de la información.
Es interesante mencionar que las hormigas sólo comenzaron a utilizar regularidades para comprimir textos muy largos. Para transmitir la información de las secuencias regulares de longitud “3” de la primera y segunda filas (Tabla 3) emplearon incluso un poco más de tiempo que en la secuencia aleatoria de igual longitud de la fila 9ª. Por tanto, a mayor tiempo empleado en la transmisión de la información, mayor información se contiene –según Kolmogorov– en el mensaje.
Agradecimientos
Estas investigaciones fueron parcialmente financiadas por el ISF (beca JFM 100) y por la Russian Foundation of Fundamental Investigations.



